Set Operations and Venn Diagrams

geeksforgeeks.org

https://www.geeksforgeeks.org/maths/set-operations…

The most common set operations, such as union, intersection, disjoint, set difference, etc., will be explored in detail below, including their definitions, examples, and Venn diagrams.

mathsisfun.com

https://www.mathsisfun.com/sets/venn-diagrams.html

Sets and Venn Diagrams - Math is Fun

A set is a collection of things. ... For example, the items you wear is a set these include hat, shirt, jacket, pants, and so on.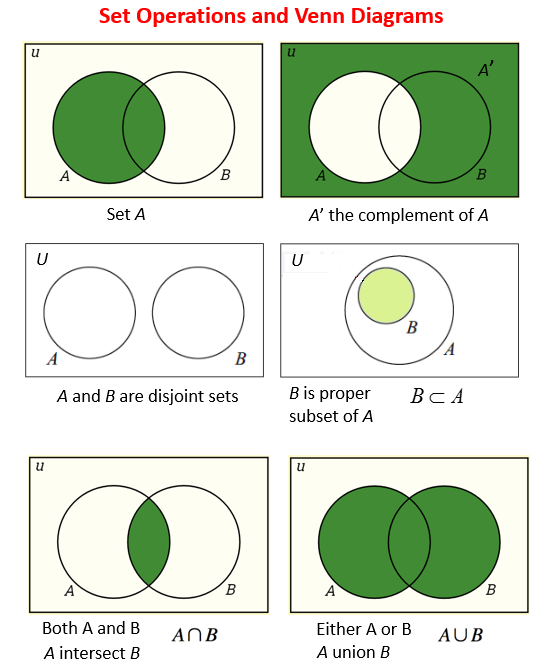

mathmonks.com

https://mathmonks.com/sets/set-operations

Set Operations - Symbols, Properties, Venn Diagram, and Examples

What are the set operations in mathematics. Learn its symbols, properties, and Venn diagrams with examples.

libretexts.org

https://math.libretexts.org/Bookshelves/Applied_Ma…

1.5: Set Operations with Three Sets - Mathematics LibreTexts

Below is a Venn diagram with two intersecting sets, which breaks the universal set up into four distinct regions. Next, we see a Venn diagram with three intersecting sets, which breaks up the universal set into eight distinct regions.

electraschematics.com

https://electraschematics.com/set-operations-and-v…

Understanding Set Operations and Venn Diagrams: A Comprehensive Guide

Venn diagrams use overlapping circles or other shapes to represent sets and their relationships. The overlapping regions of the shapes represent the elements that are common to multiple sets, while the non-overlapping regions represent elements that are unique to each set.

onlinemathlearning.com

https://www.onlinemathlearning.com/venn-diagrams.h…

Set Theory: Venn Diagrams And Subsets

The following diagrams show the set operations and Venn Diagrams for Complement of a Set, Disjoint Sets, Subsets, Intersection and Union of Sets. Scroll down the page for more examples and solutions.

tutorialspoint.com

https://www.tutorialspoint.com/discrete_mathematic…

Venn Diagrams on Sets in Discrete Mathematics

In this chapter, we explained how Venn diagrams are used to represent sets and their operations in discrete mathematics. We discussed fundamental set operations such as union, intersection, difference, and complement, and illustrated how they are visually represented in Venn diagrams.

eleccircs.com

https://eleccircs.com/venn-diagram-and-set-operati…

Understanding Venn Diagrams and Set Operations

Learn how to use Venn diagrams and perform set operations such as union, intersection, and complement to analyze and compare sets.

embibe.com

https://www.embibe.com/exams/venn-diagram-operatio…

Venn Diagram Operations on Sets: Venn Diagram, Operations - EMBIBE

John Venn popularized this method in the \ (1880 {\rm {s}}\) to help illustrate the inclusion and exclusion relationships of sets. These are also called logic diagrams, set diagrams, or primary diagrams.

autoctrls.com

https://autoctrls.com/set-operations-and-venn-diag…

Understanding Set Operations and Venn Diagrams: A Visual Approach to ...

Venn diagrams are a powerful tool for visualizing complex sets and understanding the logic behind set operations. The union of two sets is the set that contains all the elements from both sets. It can be represented by combining the circles that represent the individual sets.